En una aproximación magnetostática, el campo magnético puede ser determinado si se conoce la densidad de corriente j:
siendo:
 es el elemento diferencial de volumen.
es el elemento diferencial de volumen.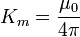 es la constante magnética.
es la constante magnética.
La divergencia y rotacional de un campo magnético estacionario puede hallarse por simple aplicación de tales operadores a la ley de Biot y Savart
Divergencia
Aplicando el operador gradiente a la expresión, se tiene:
Dado que la divergencia se aplica en un punto de evaluación del campo independiente de la integración de 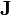 en todo el volumen, el operador no afecta a
en todo el volumen, el operador no afecta a 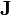 . Aplicando la correspondiente identidad vectorial:
. Aplicando la correspondiente identidad vectorial:
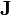 en todo el volumen, el operador no afecta a
en todo el volumen, el operador no afecta a 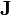 . Aplicando la correspondiente identidad vectorial:
. Aplicando la correspondiente identidad vectorial:
Dado que:
se tiene:
Rotacional
Aplicando el operador rotacional tenemos:
Al igual que ocurría en la divergencia, el operador no afecta a 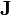 ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que
ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que 
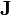 ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que
ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que 
Realizando la integración se obtiene finalmente:
Nótese que el resultado anterior sólo es válido para campos magnéticos estacionarios. Si el campo magnético no fuese estacionario aparecería aparte el término debido a la corriente de desplazamiento.


![\nabla \cdot\mathbf B=-\frac {\mu_0}{4\pi}\int_V \mathbf J \cdot \left[\nabla \times\nabla\left(\frac{1}{r}\right)\right]\ dV'](https://upload.wikimedia.org/math/8/6/f/86fd4aa5d4499f8f81e34c84020c9c49.png)





 de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales 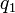 y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como: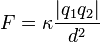


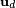 es un
es un 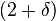
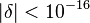

 =
=  =
=  =
=  =
= 



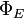 ) se mide por el número de líneas de fuerza que atraviesan la superficie.
) se mide por el número de líneas de fuerza que atraviesan la superficie. , cada uno de los cuales es lo suficientemente pequeño como para que pueda ser considerado como un plano. Estos elementos de área pueden ser representados como vectores
, cada uno de los cuales es lo suficientemente pequeño como para que pueda ser considerado como un plano. Estos elementos de área pueden ser representados como vectores  , cuya magnitud es la propia área, la dirección es perpendicular a la superficie y hacia afuera.
, cuya magnitud es la propia área, la dirección es perpendicular a la superficie y hacia afuera. . Ya que los cuadrados son tan pequeños como se quiera,
. Ya que los cuadrados son tan pequeños como se quiera,  puede considerarse constante en todos los puntos de un cuadrado dado.
puede considerarse constante en todos los puntos de un cuadrado dado. entre sí y la figura muestra una vista amplificada de dos cuadrados.
entre sí y la figura muestra una vista amplificada de dos cuadrados.

