En una aproximación magnetostática, el campo magnético puede ser determinado si se conoce la densidad de corriente j:
siendo:
es el elemento diferencial de volumen.
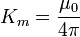es la constante magnética.
La divergencia y rotacional de un campo magnético estacionario puede hallarse por simple aplicación de tales operadores a la ley de Biot y Savart
Divergencia
Aplicando el operador gradiente a la expresión, se tiene:
Dado que la divergencia se aplica en un punto de evaluación del campo independiente de la integración de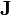 
en todo el volumen, el operador no afecta a 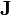. Aplicando la correspondiente identidad vectorial:
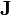en todo el volumen, el operador no afecta a 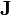. Aplicando la correspondiente identidad vectorial:![\nabla \cdot\mathbf B=-\frac {\mu_0}{4\pi}\int_V \mathbf J \cdot \left[\nabla \times\nabla\left(\frac{1}{r}\right)\right]\ dV'](https://upload.wikimedia.org/math/8/6/f/86fd4aa5d4499f8f81e34c84020c9c49.png)
Dado que:
se tiene:
Rotacional
Aplicando el operador rotacional tenemos:
Al igual que ocurría en la divergencia, el operador no afecta a 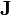ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que 
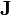ya que sus coordenadas son las del dominio de integración y no las del punto de evaluación del rotacional. Aplicando la correspondiente identidad vectorial y conociendo que 
Realizando la integración se obtiene finalmente:
Nótese que el resultado anterior sólo es válido para campos magnéticos estacionarios. Si el campo magnético no fuese estacionario aparecería aparte el término debido a la corriente de desplazamiento.
hola cual es la propiedad vectorial que usas cuando haces el rotacional de JxR?
ResponderEliminar